Policy Liberalism

This vignette demonstrates estimation of latent policy liberalism from individuals’ responses to five survey items, using the Bayesian group-level IRT model implemented in dgirt().

Prepare input data

shape() prepares input data for use with the modeling functions dgirt() and dgmrp(). Here we use the included opinion dataset.

In this call to shape() we specified:

  • the survey item response variables as item_names;
  • which variable represents time (year), since dgo models are dynamic;
  • the variables representing respondent characteristics (state and race3), because dgo models are group-level.

Notice that we named only one of these variables defining respondent groups using the group_names argument. The geo_name argument always takes the variable giving respondents’ local geographic area; it will be modeled differently.

Using the argument geo_filter, we subset the input data to the given values of the geo_name variable. And with the id_vars argument, we named an identfier that we’d like to keep in the processed data. (Other unused variables will be dropped.)

Important: the dgirt() model assumes consistent coding of the polarity of item responses for identification. This is already true for the opinion data. Typically it requires manual recoding.

Fit a model

dgirt() estimates a latent variable based on responses to multiple survey questions. Here, we’ll use it to estimate latent policy liberalism over time, for the groups defined by state and race3. (Specifically, by their Cartesian product.)

Under the hood, dgirt() uses RStan for MCMC sampling, and arguments can be passed to RStan’s stan() via the ... argument of dgirt(). This is almost always desirable. Here, we specify the number of sampler iterations, chains, and cores.

dgirt_out_liberalism <- dgirt(dgirt_in_liberalism, iter = 3000, chains = 4,
  cores = 4, seed = 42)

The model results are held in a dgirt_fit object. Methods from RStan like extract() are available if needed because dgirt_fit is a subclass of stanfit. But dgo provides its own methods for typical post-estimation tasks.

Work with results

For a high-level summary of the result, use summary().

To apply scalar functions to posterior samples, use summarize(). The default output gives summary statistics for the model’s theta_bar parameters, which represent group means. These are indexed by time (year) and group, where groups are again defined by local geographic area (state) and any other respondent characteristics (race3).

Alternatively, summarize() can apply arbitrary functions to posterior samples for whatever parameter is given by its pars argument.

To access posterior samples in tabular form use as.data.frame(). By default, this method returns post-warmup samples for the theta_bar parameters, but like other methods takes a pars argument.

To poststratify the results use poststratify(). Here, we use the group population proportions bundled as annual_state_race_targets to reweight and aggregate estimates to strata defined by state-years.

To plot the results use dgirt_plot(). This method plots summaries of posterior samples by time period. By default, it shows a 95% credible interval around posterior medians for the theta_bar parameters, for each local geographic area. Here we omit the CIs.

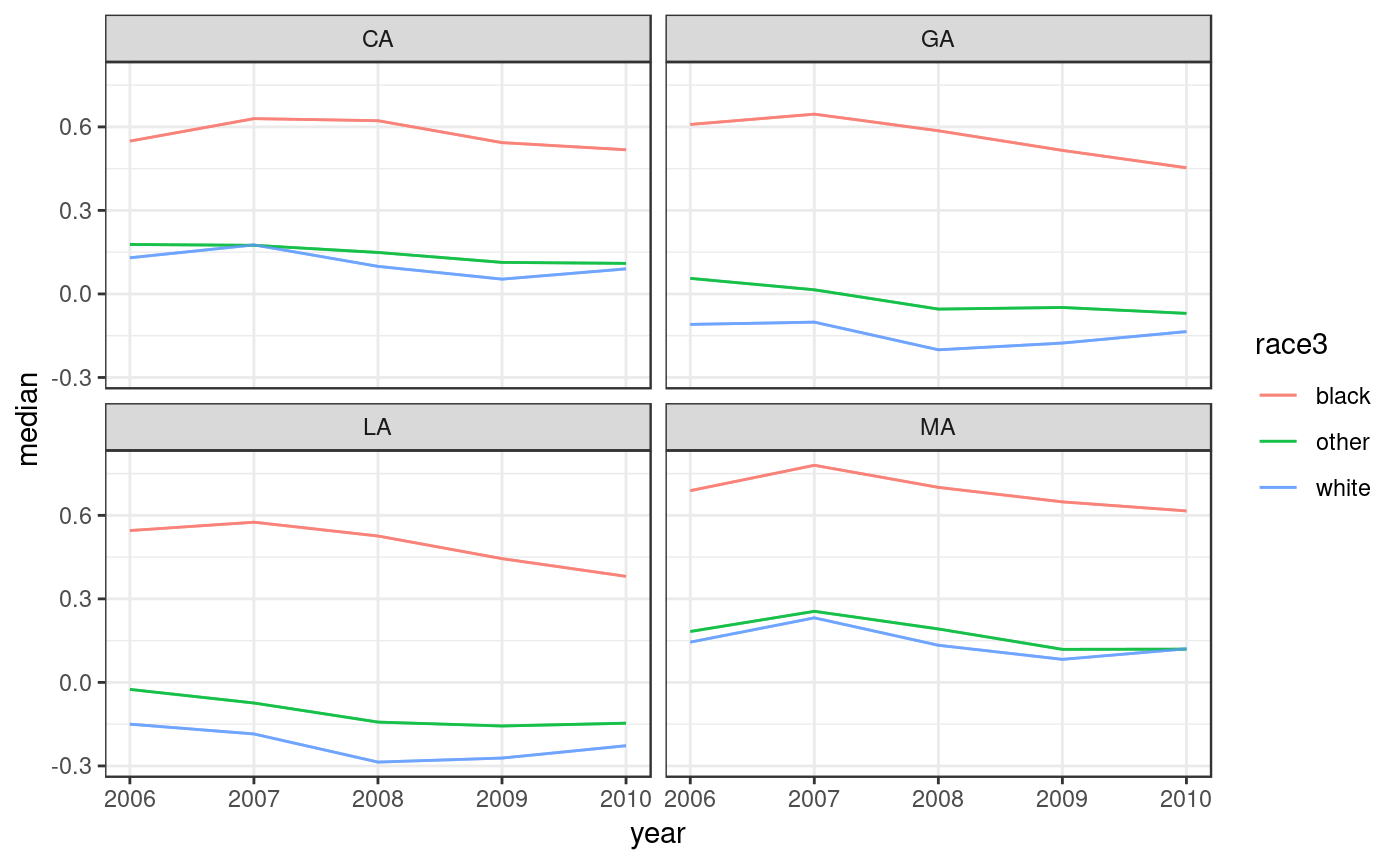
dgirt_plot(dgirt_out_liberalism, y_min = NULL, y_max = NULL)

dgirt_plot() can also plot the data.frame output from poststratify(), given arguments that identify the relevant variables. Below, we aggregate over the demographic grouping variable race3, resulting in a data.frame of estimates by state-year.

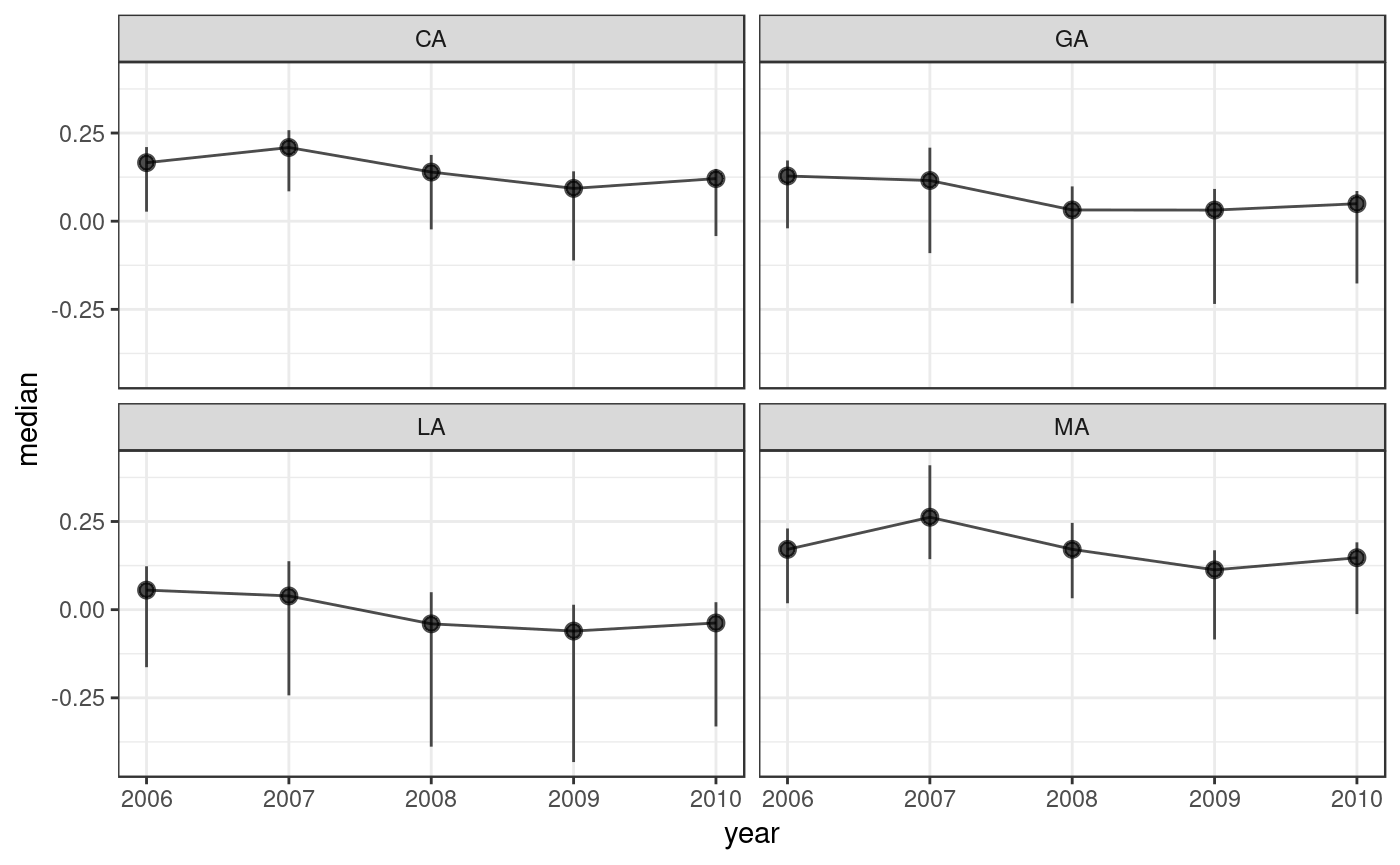
In the call to dgirt_plot(), we passed the names of the state and year variables. The group_names argument was then NULL, because there were no grouping variables left after we aggregated over race3.